Data Decomposition Algorithm Strategies and Related Coordination Strategies¶

6. Parallel For Loop Implementation Strategy: chunks of each loop per thread¶

/* parallelLoopEqualChunks.c
      * ... illustrates the use of OpenMP's default parallel for loop in which
      *       threads iterate through equal sized chunks of the index range
      *       (cache-beneficial when accessing adjacent memory locations).
      *
      * Joel Adams, Calvin College, November 2009.
      *
      * Usage: ./parallelLoopEqualChunks [numThreads]
      *
      * Exercise
      * - Compile and run, comparing output to source code
      * - try with different numbers of threads, e.g.: 2, 3, 4, 6, 8
      */

#include <stdio.h>    // printf()
      #include <stdlib.h>   // atoi()
      #include <omp.h>      // OpenMP

int main(int argc, char** argv) {
              const int REPS = 16;

printf("\n");
              if (argc > 1) {
                      omp_set_num_threads( atoi(argv[1]) );
              }

#pragma omp parallel for
              for (int i = 0; i < REPS; i++) {
                      int id = omp_get_thread_num();
                      printf("Thread %d performed iteration %d\n",
                                      id, i);
              }

printf("\n");
              return 0;
      }

Replace 4 with other values for the number of threads: 2, 3, 4, 6, 8, and re-run.

An iterative for loop is a remarkably common pattern in all programming, primarily used to perform a calculation N times, often over a set of data containing N elements, using each element in turn inside the for loop. If there are no dependencies between the calculations (i.e. the order of them is not important), then the code inside the loop can be split between forked threads. When doing this, a decision the programmer needs to make is to decide how to partition the work between the threads by answering this question:

How many and which iterations of the loop will each thread complete on its own?

We refer to this as the data decomposition strategy pattern because we are decomposing the amount of work to be done (typically on a set of data) across multiple threads. In the following code, this is done in OpenMP using the omp parallel for pragma just in front of the for statement (line 27) in the above code.

Once you run this code, verify that the default behavior for this pragma is this sort of decomposition of iterations of the loop to threads, when you set the number of threads to 4 on the command line:

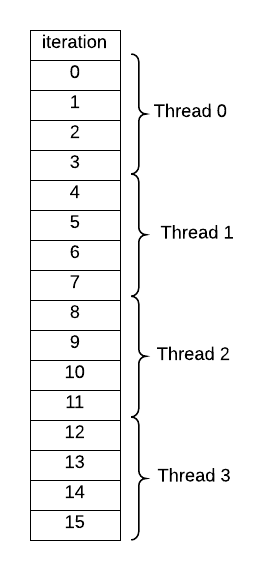
../_images/ParalleFor_Chunks-4_threads-1.png

What happens when the number of iterations (16 in this code) is not evenly divisible by the number of threads? Try several cases to be certain how the compiler splits up the work. This type of decomposition is commonly used when accessing data that is stored in consecutive memory locations (such as an array) that might be cached by each thread.

7. One iteration per thread in a parallel for loop implementation strategy¶

/* parallelLoopChunksOf1.c
      * ... illustrates how to make OpenMP map threads to
      *       parallel loop iterations in chunks of size 1
      *       (use when not accesssing memory).
      *
      * Joel Adams, Calvin College, November 2009.
      *
      * Usage: ./parallelLoopChunksOf1 [numThreads]
      *
      * Exercise:
      * 1. Compile and run, comparing output to source code,
      *    and to the output of the 'equal chunks' version.
      * 2. Uncomment the "commented out" code below,
      *    and verify that both loops produce the same output.
      *    The first loop is simpler but more restrictive;
      *    the second loop is more complex but less restrictive.
      */

#include <stdio.h>
      #include <omp.h>
      #include <stdlib.h>

int main(int argc, char** argv) {
              const int REPS = 16;

printf("\n");
              if (argc > 1) {
                      omp_set_num_threads( atoi(argv[1]) );
              }

#pragma omp parallel for schedule(static,1)
              for (int i = 0; i < REPS; i++) {
                      int id = omp_get_thread_num();
                      printf("Thread %d performed iteration %d\n",
                                      id, i);
              }

/*
              printf("\n---\n\n");

#pragma omp parallel
              {
                      int id = omp_get_thread_num();
                      int numThreads = omp_get_num_threads();
                      for (int i = id; i < REPS; i += numThreads) {
                              printf("Thread %d performed iteration %d\n",
                                              id, i);
                      }
              }
      */
              printf("\n");
              return 0;
      }

Replace 4 with other values for the number of threads.

Also try uncommenting the commented section of code and running it again.

Note

Study each of the loops very carefully in this example. You will see each one used in parallel programming examples that you may find when searching for examples. Later examples in this book also use both types of loop construction.

You can imagine other ways of assigning threads to iterations of a loop besides that shown above for four threads and 16 iterations. A simple decomposition sometimes used when your loop is not accessing consecutive memory locations would be to let each thread do one iteration, up to N threads, then start again with thread 0 taking the next iteration. This is declared in OpenMP using the pragma on line 31 of the above code. Also note that the commented code below it is an alternative explicit way of doing it. The schedule clause is the preferred style when using OpenMP and is more versatile, because you can easily change the chunk size that each thread will work on.

This can be made even more efficient if the next available thread simply takes the next iteration. In OpenMP, this is done by using dynamic scheduling instead of the static scheduling shown in the above code. We will see this shortly.

Also note that the number of iterations, or chunk size, could be greater than 1 inside the schedule clause.

8. Data Decomposition and Coordination Using Collective Communication: Reduction¶

Once threads have performed independent concurrent computations, possibly on some portion of decomposed data, it is quite common to then reduce those individual computations into one value. This type of operation is called a collective communication pattern because the threads must somehow work together to create the final desired single value.

Note the exercise for this one:

Compile and run. Note that correct output is produced. (Be sure that you know why.)
Uncomment #pragma in function parallelSum(),
but leave its reduction clause commented out
Recompile and rerun. Note that correct output is NOT produced.
Uncomment ‘reduction(+:sum)’ clause of #pragma in parallelSum()
Recompile and rerun. Note that correct output is produced again.

/* reduction.c
      * ... illustrates the OpenMP parallel-for loop's reduction clause
      *
      * Joel Adams, Calvin College, November 2009.
      *
      * Usage: ./reduction
      *
      * Exercise:
      * - Compile and run.  Note that correct output is produced.
      * - Uncomment #pragma in function parallelSum(),
      *    but leave its reduction clause commented out
      * - Recompile and rerun.  Note that correct output is NOT produced.
      * - Uncomment 'reduction(+:sum)' clause of #pragma in parallelSum()
      * - Recompile and rerun.  Note that correct output is produced again.
      */

#include <stdio.h>   // printf()
      #include <omp.h>     // OpenMP
      #include <stdlib.h>  // rand()

void initialize(int* a, int n);
      int sequentialSum(int* a, int n);
      int parallelSum(int* a, int n);

#define SIZE 1000000

int main(int argc, char** argv) {
      int array[SIZE];

if (argc > 1) {
                              omp_set_num_threads( atoi(argv[1]) );
              }

initialize(array, SIZE);
              printf("\nSeq. sum: \t%d\nPar. sum: \t%d\n\n",
                                      sequentialSum(array, SIZE),
                                      parallelSum(array, SIZE) );

return 0;
      }

/* fill array with random values */
      void initialize(int* a, int n) {
      int i;
              for (i = 0; i < n; i++) {
                      a[i] = rand() % 1000;
              }
      }

/* sum the array sequentially */
      int sequentialSum(int* a, int n) {
              int sum = 0;
              int i;
              for (i = 0; i < n; i++) {
                      sum += a[i];
              }
              return sum;
      }

/* sum the array using multiple threads */
      int parallelSum(int* a, int n) {
              int sum = 0;
              int i;
              //   #pragma omp parallel for // reduction(+:sum)
              for (i = 0; i < n; i++) {
                      sum += a[i];
              }
              return sum;
      }

In this example, an array a of randomly assigned integers represents a set of shared data (a more realistic program would perform a computation that creates meaningful data values; this is just an example). Note the common sequential code pattern found in the function called sequentialSum in the code above (starting line 50): a for loop is used to sum up all the values in the array.

Next let’s consider how this can be done in parallel with threads. Somehow the threads must implicitly communicate to keep the overall sum updated as each of them works on a portion of the array. In the parallelSum function, line 64 shows a special clause that can be used with the parallel for pragma in OpenMP for this. All values in the array are summed together by using the OpenMP parallel for pragma with the reduction(+:sum) clause on the variable sum, which is computed in line 66.

A way to visualize what is happening with this pattern is this:

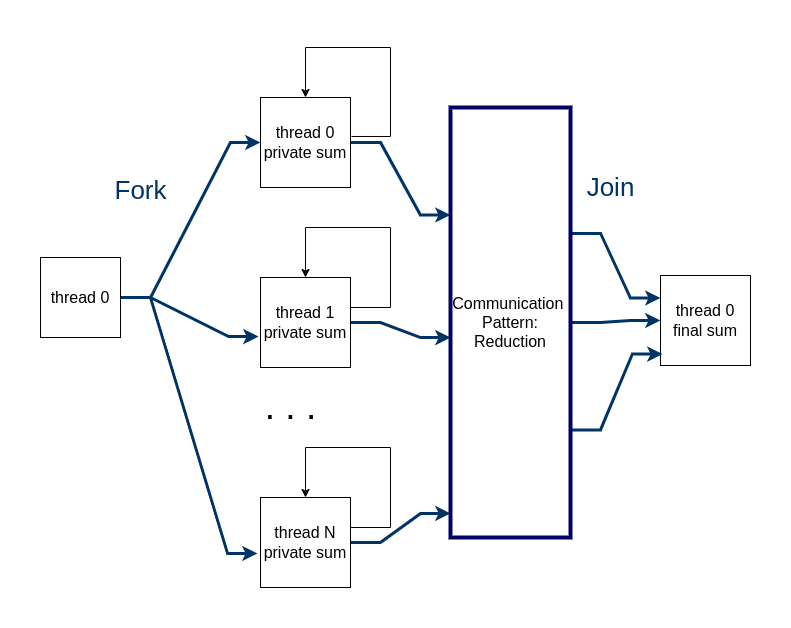
Details are left out of this picture, but from this you can realize that the threads still fork, and each one does a portion of the loop, updating its own copy of the variable sum. Then a phase of collective communication between the threads ensures that all the individual thread sums are added together and placed in a final sum on thread 0, then the threads join back together.

Note

An important method of debugging is introduced in this example. While uncommenting the portions of the pragma line in the parallelSum() function and re-running, you were able to see what the correct output should be from the sequential version. Remember this going forward as you practice more code: always devise ways to check whether your code is correct. There are different ways to accomplish this, so look for them in future examples and recall them from what you may have read in the PDC for Beginners book.

Something to think about¶

Do you have any ideas about why the parallel for pragma without the reduction clause did not produce the correct result? Later examples will hopefully shed some light on this.

Summary Overview¶

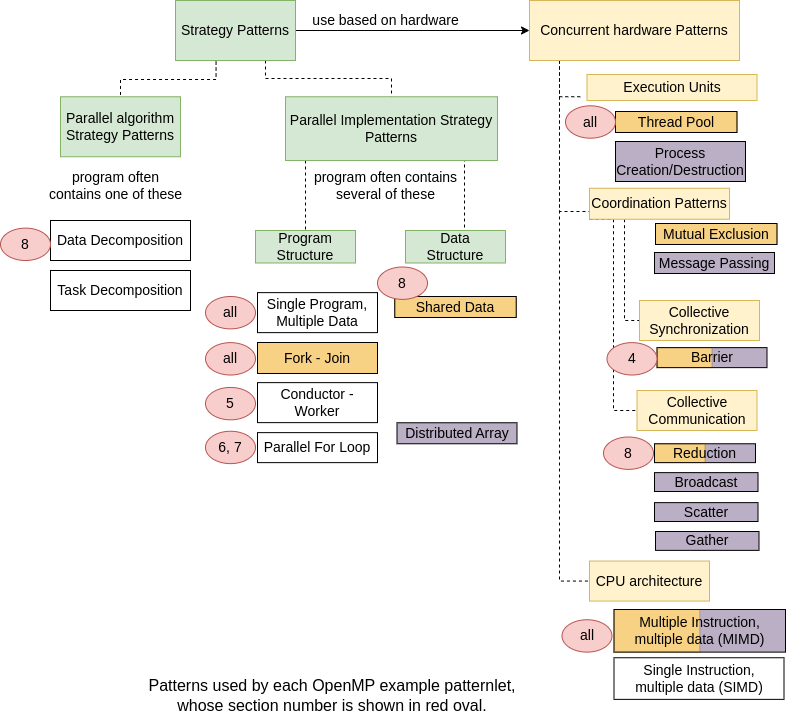
On this page we first introduced the parallel for loop implementation strategy pattern with a couple of different ways to implement it. Then you saw how this can be used on an array of data, introducing the shared data structure pattern, the data decomposition pattern and the reduction pattern, which are frequently used together. Here we have added the above examples to the diagram of the patterns.

Note

The example in section 8 is the first patternlet where truly shared memory data, in the form of array a, is used by multiple threads. This is why the Shared Data Structure pattern has now appeared.

You have attempted of activities on this page